The decoding problem
Quantum Error Correction doesn't only consist of encoding a few logical qubits into many physical qubits and detecting errors on them, but it also consists of obtaining a correction operator $C$. This correction is also a tensor product of Pauli operators on multiple qubits.
A correction $C$ for an error $E$ must fulfill the requirement that it toggles the same stabilizer measurements.
$ C E \lvert \psi \rangle = C E g_i \lvert \psi \rangle = g_i (CE \lvert \psi \rangle) \quad \forall i$
In this way, we can be sure that an error-afflicted state is once again a stabilized state. Suppose that the error commutes with the $i$-th stabilizer, then the correction must also commute with that same stabilizer:
$C E \lvert \psi \rangle = C E g_i \lvert \psi \rangle = C g_i E \lvert \psi \rangle = g_i (CE \lvert \psi \rangle)$
Said differently, if $[g_i,E]=0$ then it follows that $[g_i,C]=0$. And, if it anti-commutes with the $j$-th stabilizer, the correction must also anti-commute with that stabilizer:
$ C E \lvert \psi \rangle = C E g_j \lvert \psi \rangle = - C g_j E \lvert \psi \rangle = g_j (CE \lvert \psi \rangle) $
Which means that if $\{g_i,E\}=0$ then $\{g_i,C\}=0$.
A correction $C$ to an error $E$ is considered to be successful if one retrieves the original state of the system.
$C\lvert \psi' \rangle = C E \lvert \psi \rangle = \lvert \psi \rangle$
Conversely, it is considered to have failed if the correction applied to the error operator results in a logical error,
$ C\lvert \psi' \rangle = CE \lvert \psi \rangle = \bar{L} \lvert \psi \rangle $
for any logical operator $\bar{L}$ acting on the encoded qubit(s).
Decoding is the process through which one obtains a correction operator for a specific syndrome in a code.
In the last module we explored the action of errors on a code and observed what syndrome was obtained. Now, we engage in the opposite process: we are given a syndrome on the planar code of distance 3 and we have to guess what type of error and on which qubit the error occured. Then we can apply the right operation to correct the error.
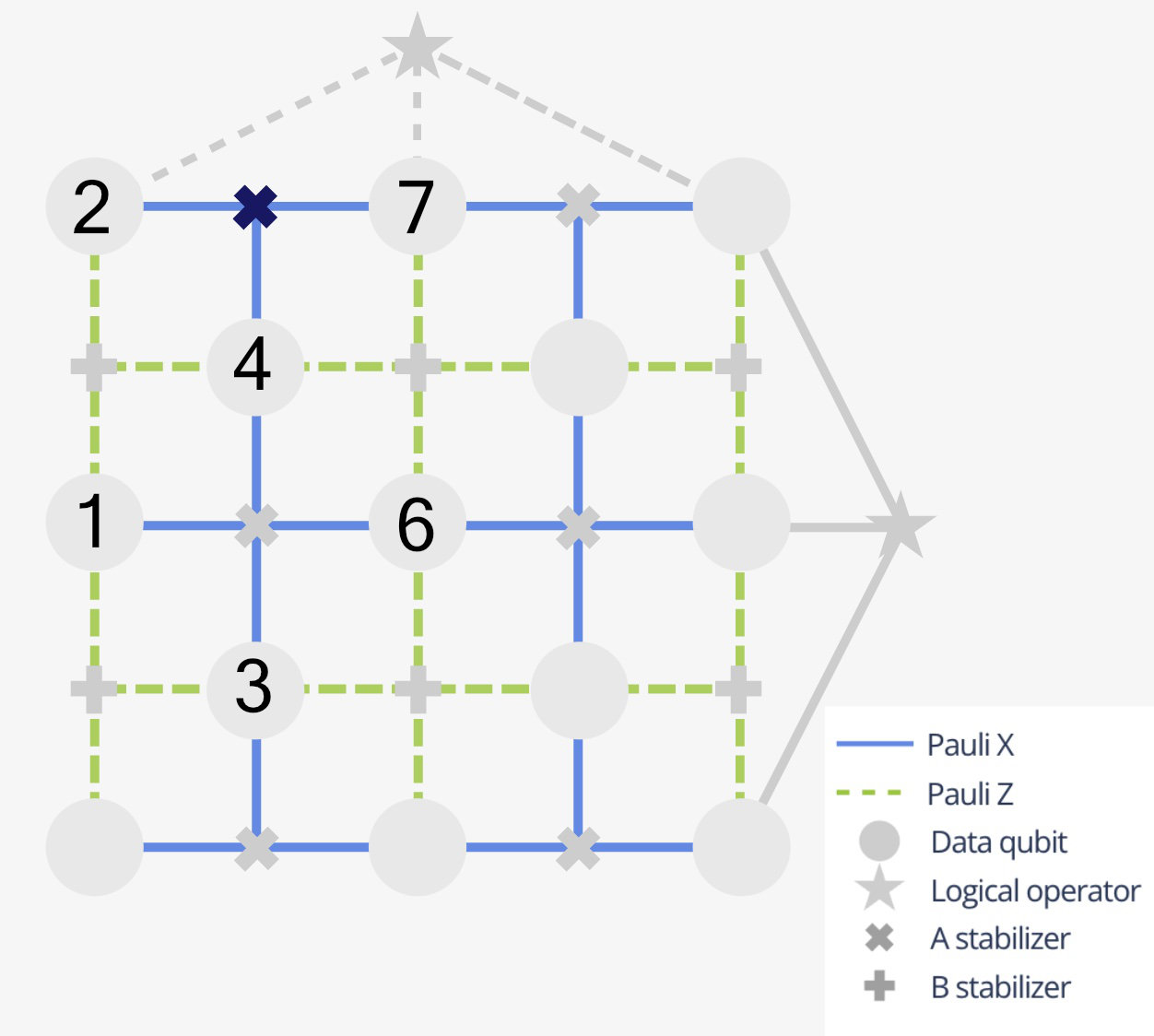
Consider the szenario in the image above. We are assuming that only one error occured. To which qubit do we need to apply which operation to correct the error?
A
Apply X to qubit 7
B
Apply Z to qubit 7
C
Apply X to qubit 2
D
Apply Z to qubit 2
E
Apply Z to qubit 4
Exploring error correction further with plaquette
