Glossary
An algorithm is a finite list of clear instructions used to solve a problem.
An
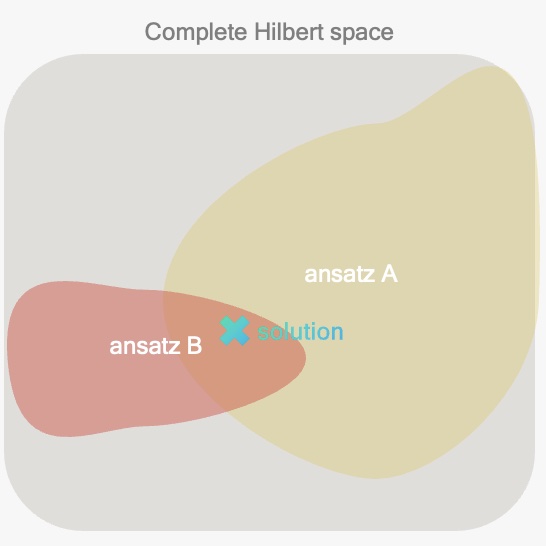
ansatz is a parametrized circuit of a specific form that is used in variational quantum algorithms. It is esentially an educated guess or approximation of a solution to the problem.
Ansätze allow us to explore different parts of the Hilbert space. In the picture above, ansatz B seems to be better suited for the problem than ansatz A. However, it is challenging finding the optimal ansatz.
Ansätze can be inspired by the physical characteristics and constraints of the quantum hardware such as the native gates or the connectivity of the quantum processing unit. They can also be derived from the particular problem one is trying to solve.
The bloch sphere is a model used to represent the state of one qubit as a point on the surface of a sphere.
Complexity classes are classes of problems that require similar resources like runtime.
Basis Encoding is a way to encode classical data into quantum states. The idea is to take the binary representation of classical data and encode it in basis states like so:
$x = \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 10_2 \\ 11_2 \end{pmatrix} \rightarrow |x\rangle = |1011\rangle$
This requires $k \cdot n$ qubits for a vector of length $k$ with $n$ binary digits each.
Amplitude Encoding is a way to encode classical data into quantum states. The idea is to take normalized classical data and encode it in state amplitudes:
$x = \begin{pmatrix} 2 \\ 1 \\ 0 \\ 3 \end{pmatrix} \rightarrow |x\rangle = \frac{1}{\sqrt{2^2 + 1^2 + 0^2 + 3^2}} \left( 2|00\rangle + 1|01\rangle + 0|10\rangle + 3|11\rangle \right)$
This requires $\lceil log(k) \rceil$ qubits for a vector of length $k$.
Angle Encoding is a way to encode classical data into quantum states. The idea is to tak normalized classical data and encode it into single qubit rotations.
This requires $k$ qubits for a vector of length $k$.
Entanglement is a phenomenon of quantum physics that is used in quantum computing. Two qubits can be entangled with each other. If we then measure the state of one of the qubits, you automatically know the state of the other qubit.
Gates are the building blocks of quantum algorithms. They are the logical representation of operations we can perform on qubits. To learn more about all the different gates, take a look at our cheat sheet for circuit magicians.
Ket notation makes use of vertical bars
$|$ and angle brackets
$\rangle$ to denote quantum states like
$|0\rangle$. Mathematically, a "ket" can be considered a vector. Two superpositional states have special symbols assigned to them in ket notation. They are obtained by applying a Hadamard gate
H to
$|0\rangle$ and
$|1\rangle$:
Observables are measurable properties of a given system in some state, like e.g. energy, momentum or position. In quantum mechanics, they are represented by Hermitian operators, which have real eigenvalues corresponding to possible outcomes of a measurement.
Optimization problems such as finding the best routes for a fleet of logistic trucks require huge resources for classical computations and are on the anticipated applications for quantum computing.
Phase is a property of quantum states and not discovered in measurements. However phase differences can be turned into measurable (amplitude) differences. For a single qubit, the phase can be thought of as the rotation angle around the north-south pole axis of the bloch sphere.
Runtime complexity of an algorithm describes how the execution time changes with the size of the input data.
Simulation of quantum systems is about simulating the behavior of things like molecules to learn more about their structure, properties, or behavior. This is very hard to do on a classical computer, thus an interesting use case for quantum computing.
A qubit can be in state $|0\rangle$, in state $|1\rangle$, or be in something called a superposition of $|0\rangle$ and $|1\rangle$. Then it has a certain probability to be measured as $|0\rangle$ or $|1\rangle$. However, a measurement destroys the superposition – i.e. all the subsequent measurements will give you the same result that you have obtained in the first place.
Machine learning describes a sub-field of artificial intelligence where the computer learns from data provided. It is another anticipated use case for quantum computing.
The parameter shift rule helps calculating the gradient of a function by evaluating the function at two different points. Unlike with finite difference, the two points don't need to be infinitesimally close to each other. It is a basic idea on how to calculate the gradient of parametrized quantum circuits.
The process of adding extra information to a message to protect it against errors is called
redundancy.
▶Quantum error correction is a set of techniques used to protect quantum information from errors.
▶ Surface codes are a type of quantum error-correcting code that use two-dimensional arrays of qubits to detect and correct errors in quantum computations.
▶ Simulatoneaous Pertubation Stochastic Approximation (SPSA) is a noise-resistant stochastic gradient approximation, which requires only two measurements of the objective function independent of the number of parameters.
The Toffoli gate (also kontrolled-controlled-not gate (CCNOT)) is a three-qubit quantum logic gate. It flips the state of the target qubit (like a NOT operation) if and only if both control qubits are in state |1⟩. In all other cases, the state of the target qubit remains unchanged.
Transpiling describes the process of converting a quantum circuit into an equivalent quantum circuit that is compatible with a specific quantum hardware's constraints and gate set.
A variational quantum circuit is a quantum circuit with gates that depend on tunable parameters. The parameter might specify the angle for a specific rotation. Note that not all gates of the circuit need to be parametrized.
There is a lot of vocabulary used in quantum computing. We help you navigate this landscape. Tell us, what you want to learn about quantum computing by writing us an email to academy@meetiqm.com.